This page explains formulas used in Jarrow-Rudd binomial option pricing model.
For similar pages for other models see Cox-Ross-Rubinstein, Leisen-Reimer.
For implementation of these formulas in Excel see Jarrow-Rudd Model in Excel.
Binomial Tree Probabilities
Like other binomial option pricing models, Jarrow-Rudd binomial trees are defined by up and down move sizes and probabilities.
The main characteristic of Jarrow-Rudd model is that up and down moves have equal probabilities: 50% each. The model is sometimes called the equal probability model.
p = 0.5
Binomial Tree Up Move
With probabilities fixed, all the inputs which describe price movement – volatility σ, risk-free interest rate r and yield q – are reflected in up and down move sizes.
Jarrow-Rudd up move formula is:

... where Δt is the duration of one step in years, calculated as the option's time to expiration t divided by the model's number of steps n:

Binomial Tree Down Move
The formula for down move is very similar:
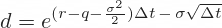
The only difference is a minus sign before the last part.
Calculating Binomial Trees
Other than these formulas, the rest of the model is the same as Cox-Ross-Rubinstein and other binomial option pricing models.
Up and down move multipliers u and d are used the generate the underlying price tree, starting from the currenct underlying price S and ending at option expiration. From each node in the tree, price can go either up (S · u) or down (S · d) to one of two nodes in the next step.
Underlying prices at expiration (the last step in the tree) are then used to calculate option payoffs at expiration, which form the last step in the option price tree.
Then the rest of the option price tree is calculated backwards, eventually reaching its first node, which is the current option price.
The entire logic and formulas are explained here:
For Excel implementation see: