This page explains the formula for kurtosis, excess kurtosis, sample kurtosis, and sample excess kurtosis. You can easily calculate all in Excel using the Descriptive Statistics Calculator.
If you don't want to go through the lengthy derivation and explanation below, the formulas are here:
Population Kurtosis Formula

Sample Kurtosis Formula

Detailed derivation and explanation of the formulas follows.
Kurtosis Definition and Use
Kurtosis is one of the summary statistics. It is used for describing or estimating relative frequency of extreme values.
Kurtosis is the ratio of (1) the fourth moment and (2) the second moment squared (= the ratio of the fourth moment and variance squared):


Deviations from the Mean
For calculating kurtosis, you first need to calculate each observation's deviation from the mean (the difference between each value and arithmetic average of all values). The deviation from the mean for ith observation equals:
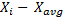
Second Moment Formula
The second moment about the mean is the sum of each value's squared deviation from the mean, divided by the number of values:
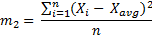
It is the same formula as the one you probably know as variance (σ2):
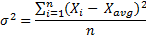
Fourth Moment Formula
The fourth moment about the mean is the sum of each value's deviation from the mean raised to the power of 4, which (the whole sum) is then divided by the number of values:

Population Kurtosis Formula
The direct kurtosis formula (ratio of the fourth moment and the second moment squared) therefore is:

The n's in the denominators cancel out and this is the final nice version of population kurtosis formula:

Excess Kurtosis Formula
Very often kurtosis is quoted in the form of excess kurtosis (kurtosis relative to normal distribution kurtosis). Excess kurtosis is simply kurtosis less 3. The excess kurtosis formula therefore is:
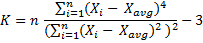
Sample Kurtosis Formula
The kurtosis and excess kurtosis formulas above are for population kurtosis (when your data set includes the whole population). Very often, you don't have data for the whole population and you need to estimate population kurtosis from a sample.
When calculating sample kurtosis, you need to make a small adjustment to the kurtosis formula:
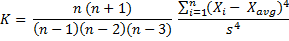
... where:
- n = sample size
- s = sample standard deviation
- s2 = sample variance:

Therefore sample kurtosis equals:


For a very large sample (very high n), the differences between n+1, n, n-1, n-2, and n-3 are becoming negligible, and the sample kurtosis formula approximately equals:

And therefore approximately equals population kurtosis formula:

Sample Excess Kurtosis Formula
Sample excess kurtosis formula differs from sample kurtosis formula only by adding a little at the end (adjusting the minus 3 for a sample):
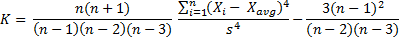
For a very large sample, the differences between and among n+1, n, n-1, n-2, and n-3 are becoming negligible, and the sample excess kurtosis formula approximately equals:

And therefore approximately equals population excess kurtosis formula:
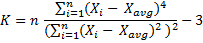
You can easily calculate kurtosis, skewness, and other measures in Excel using the Descriptive Statistics Calculator.